Напомена: ово је незванична копија задатака. Као таква, не гарантује се да ће овај сајт бити одржаван, и немојте се изненадити ако са њега задаци одједном нестану.
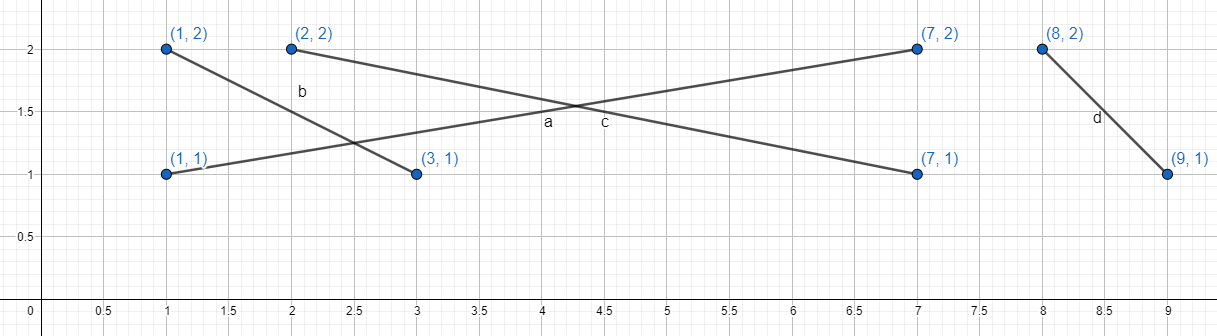
A kissé kétballábas Igor egy alkalommal megbotlott az iskolában, és elszórt egy egész doboznyi drótot. Tekintettel arra, hogy Igor különleges tanuló, a mód ahogy a drótok a padlóra hullottak is különleges. A padlót tekinthetjük koordináta-rendszernek, ahol a padló minden pontjának adott a koordinátája. Minden \(i\) -edik drót úgy esett a padlóra, hogy ábrázolhatjuk egy szakasszal, amely az \((a_i, 1)\) és \((b_i, 2)\) pontokat köti össze, vagyis a minden szakasz egyik végpontja az \(y = 1\) egyenesen, míg a másik végpontja az \(y = 2\) egyenesen helyezkedik el.
Amikor Igor ezt meglátta, teljesen elfelejtette, hová indult, és elkezdett játszani a drótokkal. Hozott egy feszültségforrást, hogy lássa, legalább hány drótot kell megérintenie, hogy mindegyik drót elektromos töltést kapjon. A drótokon nincs szigetelés, így a töltések továbbításra kerülnek egyik drótról a másikra, ha azok érintkeznek, vagyis, ha az őket képviselő szakaszok metszik egymást.
Igor sohasem foglalkozott versenyszerűen programozással, és a drótok száma is nagy, ezért a feladat megoldásához a ti segítségeteket kéri.
A bemenet első sorában egy \(N\) természetes szám, a drótok száma áll.
A második sorban \(N\) természetes számból álló sorozat \(a_1, a_2, ..., a_N\) számok állnak, a drótok végpontjának koordinátája az \(y = 1\) egyenesen.
A harmadik sorban \(N\) természetes számból álló sorozat \(b_1, b_2, ..., b_N\) számok állnak, a drótok végpontjának koordinátája az \(y = 2\) egyenesen.
A kimeneten kiíratni a szakaszok legkisebb számát, amelyet Igornak meg kell érintenie a feszültségforrással, hogy minden drót töltést kapjon!
(20 pont) \(N \leq 5000\).
(20 pont) Ha az \(i\) drótot megérintjük az áramforrással, és a töltések eljutnak a \(j\) drótra, akkor \(i\) és \(j\) érintkeznek.
(20 pont) Bármely drótot érinti meg Igor az áramforrással, a töltések legfeljebb még 5 drótot érnek el.
(40 pont) Külön korlátozások nélkül.
4
1 3 7 9
7 1 2 82Legalább két drótot meg kell érinteni, például a másodikat és negyediket. A töltések a második drótról áthaladnak az első, majd harmadik drótra.

6
7 9 8 5 4 6
9 7 8 2 3 63