The World Cup finals are approaching, and the organisers are worried about the fans’ safety – in particular, about a possible clash between the rival teams’ fans. Because of this, they decided to create a revolutionary seating arrangement.

The seats are arranged in \(N\) rows, with \(M\) seats in each. Fans can walk between seats, as well as along the outer-most seats: you can imagine this as an \(N \times M\) grid, where seats are in the middle of each cell, and the gridlines are paths. The organisers want to hire people that will sit in some of the seats and watch the four adjacent paths. They are asking you to find the minimal number of people they can hire, such that all paths are watched.

Input format

The first and only line of standard input contains two integers \(N\) and \(M\): the number of rows and columns of seats.

Output format

Your program should print one integer to the standard output: the minimal number of people the organisers must hire, such that all paths between seats are watched by at least one of them.

Sample 1

Input

5 5

Output

20

Explanation

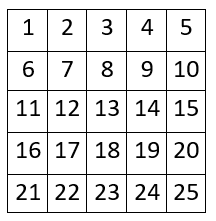
Let us number the seats as in the following image:

One option is to place the hired people in seats 1, 2, 3, 4, 5, 6, 8, 10, 11, 12, 14, 15, 16, 18, 20, 21, 22, 23, 24, 25.

Sample 2

Input

7 5

Output

27

Explanation

Let us number the seats as in the following image:

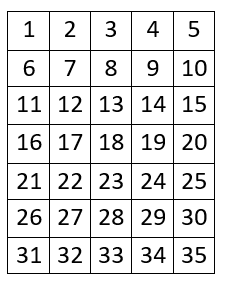
One option is to place the hired people in seats 1, 2, 3, 4, 5, 6, 8, 10, 11, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 28, 30, 31, 32, 33, 34, 35.

Constraints

• \(1 \leq N, M \leq 10^9\).

Testcases are split into five disjoint groups:

• In tests worth 20 points: \(N = 3\).
• In tests worth 20 points: \(N, M \leq 5\).
• In tests worth 20 points: \(N = M\).
• In tests worth 20 points: \(N \times M \leq 2 \times 10^5\).
• In tests worth 20 points: no additional constraints.