Közeleg a labdarúgó-világbajnokság döntője, és a szervezők aggódnak a biztonságért, mivel esélyes, hogy a két szurkolótábor összetűzésbe kerül. Ezért úgy döntöttek, hogy egy forradalmian új módszert alkalmaznak a lelátók beosztására. A lelátókon \(N\) sor található, soronként \(M\) ülőhellyel. Bármely két ülőhely között át lehet haladni, valamint a szélső helyek mellett is el lehet menni kívülről (tehát tekinthetjük egy \(N \times M\) mátrixként, ahol a pontok az ülőhelyeket, az élek pedig az útvonalakat jelölik). A szervezők néhány ülőhelyre felügyelőket szeretnének ültetni, annak érdekében, hogy minden út biztosítva legyen. Minden felügyelő 4 utat őriz a saját pozíciója körül. A szervezők arra kérnek titeket, hogy határozzátok meg, hogy ehhez legkevesebb hány felügyelő szükséges.

A bemenet leírása

A szabványos bemenet egyetlen sorában az \(N\) és \(M\) számok találhatók.

A kimenet leírása

Ki kell íratni, hogy legkevesebb hány felügyelő szükséges a lelátók biztosítására.

1. példa

Bemenet

5 5

Kimenet

20

Magyarázat

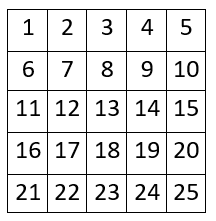
Az ülőhelyeket az alábbi módon számozzuk:

A felügyelők egyik lehetséges ültetési rendje az alábbi: 1, 2, 3, 4, 5, 6, 8, 10, 11, 12, 14, 15, 16, 18, 20, 21, 22, 23, 24, 25.

2. példa

Bemenet

7 5

Kimenet

27

Magyarázat

Az ülőhelyeket az alábbi módon számozzuk:

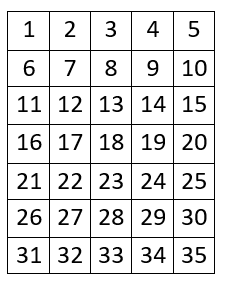
A felügyelők egyik lehetséges ültetési rendje az alábbi: 1, 2, 3, 4, 5, 6, 8, 10, 11, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 28, 30, 31, 32, 33, 34, 35.

Korlátozások

• \(1 \leq N, M \leq 10^9\).

A tesztpéldák öt diszjunkt csoportba vannak sorolva:

• A \(20\) pontot érő tesztpéldákban: \(N = 3\).
• A \(20\) pontot érő tesztpéldákban: \(N, M \leq 5\).
• A \(20\) pontot érő tesztpéldákban: \(N = M\).
• A \(20\) pontot érő tesztpéldákban: \(N \times M \leq 2 \times 10^5\).
• A \(20\) pontot érő tesztpéldákban: nincsenek további korlátozások.