Један могућ распоред редара је да се редари сместе на седишта 1, 2, 3, 4, 5, 6, 8, 10, 11, 12, 14, 15, 16, 18, 20, 21, 22, 23, 24, 25. ## Пример 2
Напомена: ово је незванична копија задатака. Као таква, не гарантује се да ће овај сајт бити одржаван, и немојте се изненадити ако са њега задаци одједном нестану.
Ближи се финале светског првенства и организатори су забринути за безбедност на трибинама. Наиме постоји шанса да дође до сукоба између навијача супарничких тимова. Зато је одлучено да се направи револуционарни распоред трибина.
Седишта трибина су распоређена у \(N\) редова са по \(M\) седишта. Могуће је пролазити између било која два седишта, као и са спољашњих страна ивичних седишта (ово можемо посматрати као \(N \times M\) матрицу, где поља представљају седишта, а ивице путеве). Организатори желе да поставе редаре на нека од седишта тако да сви путеви буду обезбеђени. Сваки редар чува 4 пута око свог седишта. Организатори од вас траже да нађете минималан број редара који је потребан да се ово уради.
У једином реду стандардног улаза се налазе бројеви \(N\) и \(M\) - број редова и број седишта по реду.
У једином реду стандардног излаза исписати минималан број редара потребан да се обезбеде трибине.
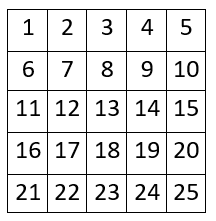
5 520Нумеришимо трибине на следећи начин:

Један могућ распоред редара је да се редари сместе на седишта 1, 2, 3,
4, 5, 6, 8, 10, 11, 12, 14, 15, 16, 18, 20, 21, 22, 23, 24, 25. ##
Пример 2
7 527Нумеришимо трибине на следећи начин:
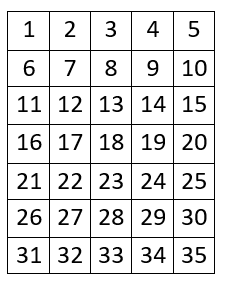
Један могућ распоред редара је да се редари сместе на седишта 1, 2, 3,
4, 5, 6, 8, 10, 11, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 28, 30,
31, 32, 33, 34, 35.
Тест примери су подељени у пет дисјунктних група: