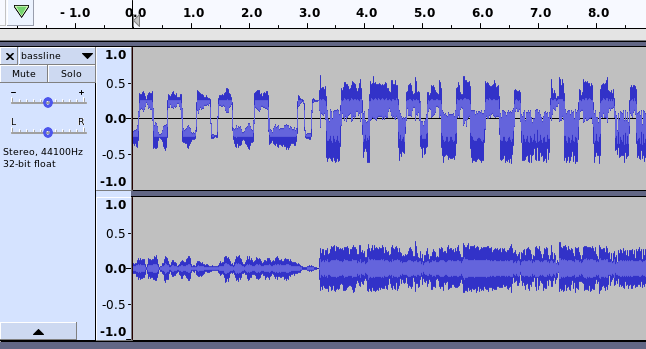
We are given a single audio file bassline.wav to investigate. If we open the file in Audacity (or plot the audio signal in some other way), we’ll see a suspicious shape in the first channel:

The long segments completely above or below 0 are definitely unexpected for an audio file and look like there is some information encoded there. The most likely choice of modulation that would cause this is something like
\[ s(t) = s_0(t) + d[\left\lfloor \frac{t}{L} \right\rfloor] \]
where \(s\) is the output signal, \(s_0\) is the song used to hide the data, \(d\) is the array of bits representing the data (where \(d[i] \in \{-1, 1\}\)) and \(L\) is the length of each encoded bit in samples.
Since the bit rate of the data is fairly low, we can separate it from the song using a low-pass filter. For example, in MATLAB:
[x, Fs] = audioread('bassline.wav');
[b, a] = butter(3, 2*20/Fs, 'low'); % 20 Hz low-pass filter
y = filter(b, a, x);
plot(y);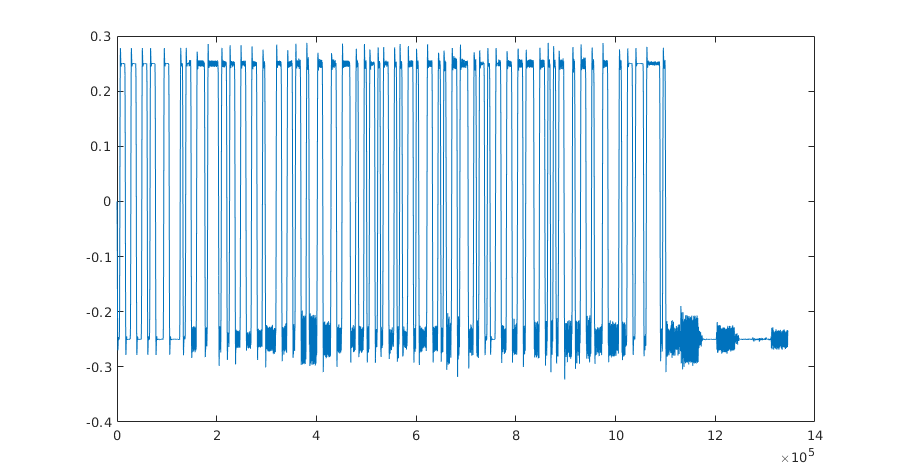
We can now get rid of the residual noise by interpreting all samples above zero as 1, and the others as 0. We will save the data to a file so we can process it later (this could be done in MATLAB, but I prefer Python for this sort of scripting):
z = y > 0;
f = fopen('bits.txt', 'w');
fprintf(f, '%d\n', z);
fclose(f);If we split the output into segments of consecutive 0 or 1-bits, we will see that their lengths are approximately 5500, 11000 and 16500. We will assume that one bit is therefore 5500 samples long and calculate the length of each segment as the closest multiple of 5500.
Now all that remains is to decode the data and convert the resulting bit-string into text:
#! /usr/bin/env python
bits = []
with open('bits.txt', 'r') as f:
for line in f:
bits.append(int(line))
cnt, curr = 0, -1
gap = 5500
res = ''
for b in bits:
if b == curr: cnt += 1
else:
for i in range((cnt + gap//2) // gap):
res += str(curr)
cnt, curr = 1, b
print(''.join(chr(int(res[i:i+8], 2)) for i in range(0, len(res), 8)))Finally, we get our flag: flag{fd3dc9-e4e7-375bda7}